Руководство по эксплуатации: Золотое сечение. Как работает золотое сечение

Эта гармония поражает своими масштабами...

Здравствуйте, друзья!

Вы что-нибудь слышали о Божественной гармонии или Золотом сечении? Задумывались ли о том, почему нам что-то кажется идеальным и красивым, а что-то отталкивает?

Если нет, то вы удачно попали на эту статью, потому что в ней мы обсудим золотое сечение, узнаем что это такое, как оно выглядит в природе и в человеке. Поговорим о его принципах, узнаем что такое ряд Фибоначчи и многое многое другое, включая понятие золотой прямоугольник и золотая спираль.

Да, в статье много изображений, формул, как-никак, золотое сечение - это еще и математика. Но все описано достаточно простым языком, наглядно. А еще, в конце статьи, вы узнаете, почему все так любят котиков =)

Что такое золотое сечение?

Если по-простому, то золотое сечение - это определенное правило пропорции, которое создает гармонию ?. То есть, если мы не нарушаем правила этих пропорций, то у нас получается очень гармоничная композиция.

Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому.

Но, кроме этого, золотое сечение - это математика: у него есть конкретная формула и конкретное число. Многие математики, вообще, считают его формулой божественной гармонии, и называют «асимметричной симметрией».

До наших современников золотое сечение дошло со времен Древней Греции, однако, бытует мнение, что сами греки уже подсмотрели золотое сечение у египтян. Потому что многие произведения искусства Древнего Египта четко построены по канонам этой пропорции.

Считается, что первым ввел понятие золотого сечения Пифагор. До наших дней дошли труды Евклида (он при помощи золотого сечения строил правильные пятиугольники, именно поэтому такой пятиугольник назван «золотым»), а число золотого сечения названо в честь древнегреческого архитектора Фидия. То есть, это у нас число «фи» (обозначается греческой буквой φ), и равно оно 1.6180339887498948482… Естественно, это значение округляют: φ = 1,618 или φ = 1,62, а в процентном соотношении золотое сечение выглядит, как 62% и 38%.

В чем же уникальность этой пропорции (а она, поверьте, есть)? Давайте для начала попробуем разобраться на примере отрезка. Итак, берем отрезок и делим его на неравные части таким образом, чтобы его меньшая часть относилась к большей, как большая ко всему целому. Понимаю, не очень пока ясно, что к чему, попробую проиллюстрировать наглядней на примере отрезков:

Итак, берем отрезок и делим его на два других, таким образом, чтобы меньший отрезок а, относился к большему отрезку b, так же, как и отрезок b относится к целому, то есть ко всей линии (a + b). Математически это выглядит так:

Этот правило работает бесконечно, вы можете делить отрезки сколь угодно долго. И, видите, как это просто. Главное один раз понять и все.

Но теперь рассмотрим более сложный пример, который попадается очень часто, так как золотое сечение еще представляют в виде золотого прямоугольника (соотношение сторон которого равно φ = 1,62). Это очень интересный прямоугольник: если от него «отрезать» квадрат, то мы снова получим золотой прямоугольник. И так бесконечно много раз. Смотрите:

Но математика не была бы математикой, если бы в ней не было формул. Так что, друзья, сейчас будет немножко «больно». Решение золотой пропорции спрятала под спойлер, очень много формул, но без них не хочу оставлять статью.

Ряд Фибоначчи и золотое сечение

Продолжаем творить и наблюдать за магией математики и золотого сечения. В средние века был такой товарищ - Фибоначчи (или Фибоначи, везде по-разному пишут). Любил математику и задачи, была у него и интересная задачка с размножением кроликов =) Но не в этом суть. Он открыл числовую последовательность, числа в ней так и зовутся «числа Фибоначчи».

Сама последовательность выглядит так:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233... и дальше до бесконечности.

Если словами, то последовательность Фибоначчи - это такая последовательность чисел, где каждое последующее число, равно сумме двух предыдущих.

Причем здесь золотое сечение? Сейчас увидите.

Спираль Фибоначчи

Чтобы увидеть и прочувствовать всю связь числового ряда Фибоначчи и золотого сечения, нужно снова взглянуть на формулы.

Иными словами, с 9-го члена последовательности Фибоначчи мы начинаем получать значения золотого сечения. И если визуализировать всю эту картину, то мы увидим, как последовательность Фибоначчи создает прямоугольники все ближе и ближе к золотому прямоугольнику. Вот такая вот связь.

Теперь поговорим о спирали Фибоначчи, ее еще называют «золотой спиралью».

Золотая спираль - логарифмическая спираль, коэффициент роста которой равен φ4, где φ - золотое сечение.

В общем и целом, с точки зрения математики, золотое сечение - идеальная пропорция. Но на этом ее чудеса только начинаются. Принципам золотого сечения подчинен почти весь мир, эту пропорцию создала сама природа. Даже эзотерики, и те, видят в ней числовую мощь. Но об этом точно не в этой статье будем говорить, поэтому, чтобы ничего не пропустить, можете подписаться на обновления сайта.

Золотое сечение в природе, человеке, искусстве

Прежде, чем мы начнем, хотелось бы уточнить ряд неточностей. Во-первых, само определение золотого сечения в данном контексте не совсем верно. Дело в том, что само понятие «сечение» - это термин геометрический, обозначающий всегда плоскость, но никак не последовательность чисел Фибоначчи.

И, во-вторых, числовой ряд и соотношение одного к другому, конечно, превратили в некий трафарет, который можно накладывать на все, что кажется подозрительным, и очень радоваться, когда есть совпадения, но все же, здравый смысл терять не стоит.

Однако, «все смешалось в нашем королевстве» и одно стало синонимом другого. Так что в общем и целом, смысл от этого не потерялся. А теперь к делу.

Вы удивитесь, но золотое сечение, точнее пропорции максимально приближенные к нему, можно увидеть практически везде, даже в зеркале. Не верите? Давайте с этого и начнем.

Знаете, когда я училась рисовать, то нам объясняли, как проще строить лицо человека, его тело и прочее. Все надо рассчитывать, относительно чего-то другого.

Все, абсолютно все пропорционально: кости, наши пальцы, ладони, расстояния на лице, расстояние вытянутых рук по отношению к телу и так далее. Но даже это не все, внутреннее строение нашего организма, даже оно, приравнивается или почти приравнивается к золотой формуле сечения. Вот какие расстояния и пропорции:

от плеч до макушки к размеру головы = 1:1.618

от пупка до макушки к отрезку от плеч до макушки = 1:1.618

от пупка до коленок и от коленок до ступней = 1:1.618

от подбородка до крайней точки верхней губы и от нее до носа = 1:1.618

Разве это не удивительно!? Гармония в чистом виде, как внутри, так и снаружи. И именно поэтому, на каком-то подсознательном что-ли уровне, некоторые люди не кажутся нам красивыми, даже если у них крепкое подтянутое тело, бархатная кожа, красивые волосы, глаза и прочее и все остальное. Но, все равно, малейшее нарушений пропорций тела, и внешность уже слегка «режет глаза».

Короче говоря, чем красивее кажется нам человек, тем ближе его пропорции к идеальным. И это, кстати, не только к человеческому телу можно отнести.

Золотое сечение в природе и ее явлениях

Классическим примером золотого сечения в природе является раковина моллюска Nautilus pompilius и аммонита. Но это далеко не все, есть еще много примеров:

в завитках человеческого уха мы можем увидеть золотую спираль;

ее же (или приближенную к ней) в спиралях, по которым закручиваются галактики;

и в молекуле ДНК;

по ряду Фибоначчи устроен центр подсолнуха, растут шишки, середина цветов, ананас и многие другие плоды.

Друзья, примеров настолько много, что я просто оставлю тут видеоролик (он чуть ниже), чтобы не перегружать текстом статью. Потому что, если эту тему копать, то можно углубиться в такие дебри: еще древние греки доказывали, что Вселенная и, вообще, все пространство, - спланировано по принципу золотого сечения.

Вы удивитесь, но эти правила можно отыскать даже в звуке. Смотрите:

Наивысшая точка звука, вызывающая боль и дискомфорт в наших ушах, равна 130 децибелам.

Делим пропорцией 130 на число золотого сечения φ = 1,62 и получаем 80 децибел - звук человеческого крика.

Продолжаем пропорционально делить и получаем, скажем так, нормальную громкость человеческой речи: 80 / φ = 50 децибел.

Ну, а последний звук, который получим благодаря формуле – приятный звук шепота = 2,618.

По данному принципу можно определить оптимально-комфортное, минимальное и максимальное число температуры, давления, влажности. Я не проверяла, и не знаю, насколько эта теория верна, но, согласитесь, звучит впечатляюще.

Абсолютно во всем живом и не живом можно прочесть высшую красоту и гармонию.

Главное, только не увлекаться этим, ведь если мы хотим что-то в чем-то увидеть, то увидим, даже если этого там нет. Вот я, например, обратила внимание на дизайн PS4 и увидела там золотое сечение =) Впрочем, эта консоль настолько классная, что не удивлюсь, если дизайнер, и правда, что-то там мудрил.

Золотое сечение в искусстве

Тоже очень большая и обширная тема, которую стоит рассмотреть отдельно. Тут лишь помечу несколько базовых моментов. Самое примечательное, что многие произведения искусства и архитектурные шедевры древности (и не только) сделаны, по принципам золотого сечения.

Египетские и пирамиды Майя, Нотр-дам де Пари, греческий Парфенон и так далее.

В музыкальных произведениях Моцарта, Шопена, Шуберта, Баха и прочих.

В живописи (там это наглядно видно): все самые знаменитые картины известных художников сделаны с учетом правил золотого сечения.

Эти принципы можно встретить и в стихах Пушкина, и в бюсте красавицы Нефертити.

Даже сейчас правила золотой пропорции используются, например, в фотографии. Ну, и конечно, во всем остальном искусстве, включая кинематограф и дизайн.

Золотые котики Фибоначчи

Ну и, наконец, о котиках! Вы задумывались о том, почему все так любят котеек? Они же ведь заполонили Интернет! Котики везде и это чудесно =)

А все дело в том, что кошки - идеальны! Не верите? Сейчас докажу вам это математически!

Видите? Тайна раскрыта! Котейки идеальны с точки зрения математики, природы и Вселенной =)

* Я шучу, конечно. Нет, кошки, действительно, идеальны) Но математически их никто не измерял, наверное.

На этом, в общем-то, все, друзья! Мы увидимся в следующих статьях. Удачи вам!

P. S. Изображения взяты с сайта medium.com.

Золотое сечение - это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве – во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.

Определение

Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому. Приблизительная его величина – 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени. Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как «ассиметричную симметрию», называя его в широком смысле универсальным правилом отражающим структуру и порядок нашего мироустройства.

История

Принято считать, что понятие о золотом делении ввёл в научный обиход Пифагор , древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор своё знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзьенашёл, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображённый на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.

Платон (427...347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящён математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.

В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.

Рис. Античный циркуль золотого сечения

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида . Во 2-й книге «Начал» даётся геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвящённым.

Представление о золотых пропорциях имели и на Руси, но впервые научно золотое сечение объяснил монах Лука Пачоли в книге «Божественная пропорция» (1509), иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял Сына, большой – Отца, а целое – Святой дух. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.

Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи . В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности». Сейчас ряд Фибоначчи это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.

Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.

Со временем правило золотого сечения превратилось в академическую рутину, и только философ Адольф Цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его «математическое эстетство» вызывало много критики.

Природа

Астроном XVI в. Иоганн Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).

Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причём та же пропорция сохраняется до бесконечности».

Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).

Если на прямой произвольной длины, отложить отрезок m , рядом откладываем отрезок M . На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов.

Рис. Построение шкалы отрезков золотой пропорции

Рис. Цикорий

Даже не вдаваясь в расчеты, золотое сечение можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть.

Рис. Ящерица живородящая

Рис. Яйцо птицы

Белорусский ученый Эдуард Сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.

Еще Архимед , уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гёте отмечал тяготение природы к спиральным формам, называя спираль «кривой жизни» . Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.

Человек

Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек – это универсальная форма для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды.

В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях. Опираясь на исследования римского архитектора Витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле Корбюзье, используя «Витрувианского человека» Леонардо, создал собственную шкалу «гармонических пропорций», повлиявшую на эстетику архитектуры XX века. Адольф Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа.

В результате измерений исследователь установил, что пропорции мужского тела 13:8 ближе к золотому сечению, чем пропорции женского тела – 8:5.

Искусство пространственных форм

Художник Василий Суриков говорил, «что в композиции есть непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже лишнюю точку поставить нельзя, это настоящая математика». Долгое время художники следователи этому закону интуитивно, но после Леонардо да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек золотого сечения использовал изобретенный им пропорциональный циркуль.

Искусствовед Ф. В. Ковалев, подробно исследовав картину Николая Ге «Александр Сергеевич Пушкин в селе Михайловском», отмечает, что каждая деталь полотна будь-то камин, этажерка, кресло или сам поэт строго вписаны в золотые пропорции. Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы , Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.

И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.

Гёте, поэт, естествоиспытатель и художник (он рисовал и писал акварелью), мечтал о создании единого учения о форме, образовании и преобразовании органических тел. Это он ввёл в научный обиход термин морфология .

Пьер Кюри в начале нашего столетия сформулировал ряд глубоких идей симметрии. Он утверждал, что нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды.

Закономерности «золотой» симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.

Золотое сечение и симметрия

Золотое сечение нельзя рассматривать само по себе, отдельно, без связи с симметрией. Великий русский кристаллограф Г.В. Вульф (1863...1925) считал золотое сечение одним из проявлений симметрии.

Золотое деление не есть проявление асимметрии, чего-то противоположного симметрии. Согласно современным представлениям золотое деление – это асимметричная симметрия. В науку о симметрии вошли такие понятия, как статическая и динамическая симметрия . Статическая симметрия характеризует покой, равновесие, а динамическая – движение, рост. Так, в природе статическая симметрия представлена строением кристаллов, а в искусстве характеризует покой, равновесие и неподвижность. Динамическая симметрия выражает активность, характеризует движение, развитие, ритм, она – свидетельство жизни. Статической симметрии свойственны равные отрезки, равные величины. Динамической симметрии свойственно увеличение отрезков или их уменьшение, и оно выражается в величинах золотого сечения возрастающего или убывающего ряда.

Слово, звук и кинолента

Формы временно̀го искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи – 5, 8, 13, 21, 34.

Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом «Пиковой дамы» является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853:535=1,6) – это и есть точка золотого сечения.

Советский музыковед Э. К. Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера. Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение.

Кинорежиссер Сергей Эйзенштейн сценарий своего фильма «Броненосец Потёмкин» сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей. В первых трех разделах действие разворачивается на корабле, а в последних двух – в Одессе. Переход на сцены в городе и есть золотая середина фильма.

Приглашаем к обсуждению темы в нашей группе -

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором меньший отрезок так относится к большему, как больший ко всему.

a: b = b: c или с: b = b: а.

Эта пропорция равна:

К примеру, в правильной пятиконечной звезде, каждый сегмент делится пересекающим его сегментом в золотом сечении (т. е. отношение синего отрезка к зелёному, красного к синему, зелёного к к фиолетовому, равны 1.618

Принято считать, что понятие о золотом сечении ввел в научный обиход Пифагор. Есть предположение, что Пифагор свое знание позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования» .
Цейзинг измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон.

Золотые пропорции в частях тела человека

Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13: 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8: 5 = 1,6.

У новорожденного пропорция составляет отношение 1: 1, к 13 годам она равна 1,6, а к 21 году равняется мужской.
Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.
Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры.

Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи .

Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления.

Так, 21: 34 = 0,617, а 34: 55 = 0,618. (или 1.618 , если делить большее число на меньшее).

Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого сечения.

Золотое сечение в искусстве

Еще в 1925 году искусствовед Л.Л.Сабанеев, проанализировав 1770 музыкальных произведений 42 авторов, показал, что подавляющее большинство выдающихся сочинений можно легко разделить на части или по теме, или по интонационному строю, или по ладовому строю, которые находятся между собой в отношении золотого сечения.

Причем, чем талантливее композитор, тем в большем количестве его произведений найдено золотых сечений. У Аренского, Бетховена, Бородина, Гайдна, Моцарта, Скрябина, Шопена и Шуберта золотые сечения найдены в 90% всех произведений. По мнению Сабанеева, золотое сечение приводит к впечатлению особой стройности музыкального сочинения.

В кино С. Эйзенштейн искусственно построил фильм Броненосец Потёмкин по правилам «золотого сечения». Он разбил ленту на пять частей. В первых трёх действие разворачивается на корабле. В двух последних - в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения.

Золотое сечение в архитектуре, скульптуре, живописи

Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).

На рисунках виден целый ряд закономерностей, связанных с золотым сечением. Пропорции здания можно выразить через различные степени числа Ф=0,618...

На плане пола Парфенона также можно заметить "золотые прямоугольники":

Золотое соотношение мы можем увидеть и в здании собора Парижской Богоматери (Нотр-дам де Пари), и в пирамиде Хеопса:

Не только египетские пиpамиды постpоены в соответствии с совеpшенными пpопоpциями золотого сечения; то же самое явление обнаpужено и у мексиканских пиpамид.

Золотая пропорция применялась многими античными скульпторами. Известна золотая пропорция статуи Аполлона Бельведерского: рост изображенного человека делится пупочной линией в золотом сечении.

Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Посмотрим внимательно на картину "Джоконда". Композиция портрета построена на"золотых треугольниках".

Золотое сечение в шрифтах и бытовых предметах

Золотое сечение в живой природе

В биологических исследованиях было показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем.

Было установлено, что числовой ряд чисел Фибоначчи характеризует структурную организацию многих живых систем. Например, винтовое листорасположение на ветке составляет дробь (число оборотов на стебле/число листьев в цикле, напр. 2/5; 3/8; 5/13), соответствующую рядам Фибоначчи.

Хорошо известна "золотая" пропорция пятилепестковых цветков яблони, груши и многих других растений. Носители генетического кода - молекулы ДНК и РНК - имеют структуру двойной спирали; ее размеры почти полностью соответствуют числам ряда Фибоначчи.

Гете подчеркивал тенденцию природы к спиральности.

Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали.

Гете называл спираль "кривой жизни". Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д.

Цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках "упакованы" по логарифмическим ("золотым") спиралям, завивающимся навстречу друг другу, причем числа "правых "и "левых" спиралей всегда относятся друг к другу, как соседние числа Фибоначчи.

Рассмотрим побег цикория. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс.

Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

У многих бабочек соотношение размеров грудной и брюшной части тела отвечает золотой пропорции. Сложив крылья, ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2,3,5,8. Стрекоза также создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.

В ящерице длина ее хвоста так относится к длине остального тела, как 62 к 38. Можно заметить золотые пропорции, если внимательно посмотреть на яйцо птицы.

Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определённом отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.

Золотое сечение – гармоническая пропорция

В математике пропорцией (лат. proportio) называют равенство двух отношений:

a : b = c : d .

Отрезок прямой AB можно разделить на две части следующими способами:

на две равные части – AB : AC = AB : BC ;
на две неравные части в любом отношении (такие части пропорции не образуют);
таким образом, когда AB : AC = AC : BC .

Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему:

a : b = b : c
или
c : b = b : a .

Рис. 1. Геометрическое изображение золотой пропорции

Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.

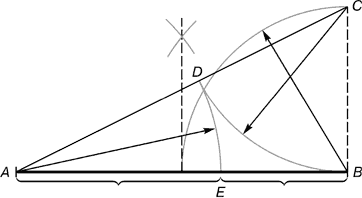
Рис. 2. BC = 1/2 AB ; CD = BC

Из точки B восставляется перпендикуляр, равный половине AB . Полученная точка C соединяется линией с точкой A . На полученной линии откладывается отрезок BC , заканчивающийся точкой D . Отрезок AD переносится на прямую AB . Полученная при этом точка E делит отрезок AB в соотношении золотой пропорции.

Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618..., если AB принять за единицу, BE = 0,382... Для практических целей часто используют приближённые значения 0,62 и 0,38. Если отрезок AB принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.

Свойства золотого сечения описываются уравнением:

x 2 – x – 1 = 0.

Решение этого уравнения:

Свойства золотого сечения создали вокруг этого числа романтический ореол таинственности и чуть ли не мистического поклонения.

Второе золотое сечение

Болгарский журнал «Отечество» (№10, 1983 г.) опубликовал статью Цветана Цекова-Карандаша «О втором золотом сечении», которое вытекает из основного сечения и даёт другое отношение 44: 56.

Такая пропорция обнаружена в архитектуре, а также имеет место при построении композиций изображений удлинённого горизонтального формата.

Рис. 3.

Деление осуществляется следующим образом. Отрезок AB делится в пропорции золотого сечения. Из точки C восставляется перпендикуляр CD . Радиусом AB находится точка D , которая соединяется линией с точкой A . Прямой угол ACD делится пополам. Из точки C проводится линия до пересечения с линией AD . Точка E делит отрезок AD в отношении 56: 44.

Рис. 4.

На рисунке показано положение линии второго золотого сечения. Она находится посередине между линией золотого сечения и средней линией прямоугольника.

Золотой треугольник

Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой .

Рис. 5. Построение правильного пятиугольника и пентаграммы

Для построения пентаграммы необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471...1528). Пусть O – центр окружности, A – точка на окружности и E – середина отрезка OA . Перпендикуляр к радиусу OA , восставленный в точке O , пересекается с окружностью в точке D . Пользуясь циркулем, отложим на диаметре отрезок CE = ED . Длина стороны вписанного в окружность правильного пятиугольника равна DC . Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.

Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит её в пропорции золотого сечения.

Рис. 6. Построение золотого треугольника

Проводим прямую AB . От точки A откладываем на ней три раза отрезок O произвольной величины, через полученную точку P проводим перпендикуляр к линии AB , на перпендикуляре вправо и влево от точки P откладываем отрезки O . Полученные точки d и d 1 соединяем прямыми с точкой A . Отрезок dd 1 откладываем на линию Ad 1 , получая точку C . Она разделила линию Ad 1 в пропорции золотого сечения. Линиями Ad 1 и dd 1 пользуются для построения «золотого» прямоугольника.

История золотого сечения

Принято считать, что понятие о золотом делении ввёл в научный обиход Пифагор , древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор своё знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса , храмов, барельефов, предметов быта и украшений из гробницы свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашёл, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображённый на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

Рис. 7. Динамические прямоугольники

Платон (427...347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящён математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.

Рис. 8.

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида . Во 2-й книге «Начал» даётся геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвящённым.

В эпоху Возрождения усиливается интерес к золотому делению среди учёных и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи , художник и учёный, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески , написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.

Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г. по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и её «божественную суть» как выражение Божественного Триединства – Бог Отец , Бог Сын и Бог Дух Святой (подразумевалось, что малый отрезок есть олицетворение Бога Сына, больший отрезок – Бога Отца, а весь отрезок – Бога Духа Святого).

Электронные книги:

Марио Ливио.

Кандидат технических наук В. БЕЛЯНИН, ведущий научный сотрудник РНЦ "Курчатовский институт", Е. РОМАНОВА, студентка МАДИ (ГТУ)

Наука и жизнь // Иллюстрации

Золотую пропорцию в школе не "проходят". И когда один из авторов предлагаемой ниже статьи (кандидат технических наук В. Белянин) рассказал о золотом сечении абитуриентке, собравшейся поступать в МАДИ, в процессе подготовки к экзаменам в институт, задача неожиданно вызвала живой интерес и массу вопросов, на которые "с ходу" не было ответов. Решили искать их вместе, и тогда обнаружились тонкости в золотой пропорции, ускользавшие от исследователей ранее. Совместное творчество привело к работе, которая лишний раз подтверждает созидательные возможности молодежи и вселяет надежду, что язык науки утерян не будет.

Узоры математики, как и узоры художника или узоры поэта, должны быть красивы; идеи, как и краски или слова, должны сочетаться гармонически. Красота является первым критерием: в мире нет места для безобразной математики.
Дж. Х. Харди

Красота математической задачи служит одним из важнейших стимулов ее нескончаемого развития и причиной порождения многочисленных приложений. Порой проходят десятки, сотни, а иногда и тысячи лет, но люди вновь и вновь находят неожиданные повороты в хорошо известном решении и его интерпретации. Одной из таких долгоживущих и увлекательных задач оказалась задача о золотом сечении (ЗС), отражающая элементы изящества и гармонии окружающего нас мира. Нелишне напомнить, кстати, что, хотя сама пропорция была известна еще Евклиду, термин "золотое сечение" ввел Леонардо да Винчи (см. "Наука и жизнь" ).

Геометрически золотое сечение подразумевает деление отрезка на две неравные части так, чтобы большая часть была средним пропорциональным между всем отрезком и меньшей частью (рис. 1).

Алгебраически это выражается следующим образом:

Исследование этой пропорции еще до ее решения показывает, что между отрезками a и b существуют по крайней мере два удивительных соотношения. Например, из пропорции (1) легко получается выражение,

которое устанавливает пропорцию между отрезками a , b , их разностью и суммой. Поэтому о золотом сечении можно сказать иначе: два отрезка находятся в гармоничном соотношении, если их разность относится к меньшему отрезку так, как больший отрезок относится к их сумме.

Второе соотношение получается, если исходный отрезок принять равным единице: a + b = 1, что очень часто используется в математике. В таком случае

a 2 - b 2 = a - b = ab .

Из этих результатов следуют два удивительных соотношения между отрезками а и b :

a 2 - b 2 = a - b = ab ,(2)

которые будут использованы в дальнейшем.

Перейдем теперь к решению пропорции (1). На практике используют две возможности.

1. Обозначим отношение a /b через. Тогда получим уравнение

x 2 - x - 1 = 0, (3)

Обычно рассматривают только положительный корень x 1 , дающий простое и наглядное деление отрезка в заданной пропорции. Действительно, если принять целый отрезок за единицу, то, используя значение этого корня x 1 , получим a ≈ 0,618, b ≈ 0,382.

Именно положительный корень x 1 уравнения (3) наиболее часто называют золотой пропорцией или пропорцией золотого сечения. Соответствующее геометрическое деление отрезка называют золотым сечением (точка С на рис. 1).

Для удобства дальнейшего изложения обозначим x 1 = D . Общепризнанного обозначения для золотого сечения до сих пор нет. Обусловлено это, видимо, тем, что под ним понимают иногда и другое число, о чем будет сказано ниже.

Оставляемый по обыкновению в стороне отрицательный корень x 2 приводит к менее наглядному делению отрезка на две неравные части. Дело в том, что он дает делящую точку С , которая лежит вне отрезка (так называемое внешнее деление). Действительно, если a + b = 1, то, используя корень x 2 , получим a ≈ -1,618, b ≈ 2,618. Поэтому отрезок a необходимо откладывать в отрицательном направлении (рис. 2).

2. Второй вариант решения пропорции (1) принципиально не отличается от первого. Будем считать неизвестным отношение b /a и обозначим его через y . Тогда получим уравнение

y 2 + y -1 = 0 , (4)

которое имеет иррациональные корни

Если a + b = 1, то, используя корень y 1 , получим a = y 1 ≈ 0,618, b ≈ 0,382. Для корня y 2 получим a ≈ -1,618, b ≈ 2,618. Геометрическое деление отрезка в пропорции золотого сечения с использованием корней y 1 и y 2 полностью идентично предыдущему варианту и соответствует рис. 1 и 2.

Положительный корень y 1 непосредственно дает искомое решение задачи, и его также называют золотой пропорцией .

Для удобства обозначим значение корня y 1 = d.

Таким образом, в литературе золотую пропорцию математически выражают числом D 1,618 или числом d 0,618, между которыми существуют две изумительные связи:

Dd = 1 и D - d = 1. (5)

Доказано, что другой подобной пары чисел, обладающих этими свойствами, не существует.

Используя оба обозначения для золотой пропорции, запишем решения уравнений (3) и (4) в симметричном виде: = D , = -d , = d , = -D .

Необычные свойства золотого сечения достаточно подробно описаны в литературе . Они настолько удивительны, что покоряли разум многих выдающихся мыслителей и создали вокруг себя ореол таинственности.

Золотая пропорция встречается в конфигурации растений и минералов, строении частей Вселенной, музыкальном звукоряде. Она отражает глобальные принципы природы, пронизывая все уровни организации живых и неживых объектов. Ее используют в архитектуре, скульптуре, живописи, науке, вычислительной технике, при проектировании предметов быта. Творения, несущие в себе конфигурацию золотого сечения, представляются соразмерными и согласованными, всегда приятны взгляду, да и сам математический язык золотой пропорции не менее изящен и элегантен.

Кроме равенств (5) из соотношения (2) можно выделить три интересные соотношения, которые обладают определенным совершенством, выглядят вполне привлекательно и эстетично:

(6)

Величие и глубину природы можно ощущать не только, например, при созерцании звезд или горных вершин, но и вглядываясь в некоторые удивительные формулы, очень ценимые математиками за их красоту. К ним можно отнести изящные соотношения золотой пропорции, фантастическую формулу Эйлера e iπ = -1 (где i = √-1), формулу, определяющую знаменитое число Непера (основание натуральных логарифмов): e = lim(1 + 1/n ) n = 2,718 при n → ∞, и многие другие.

После решения пропорции (1) ее идея кажется довольно простой, но, как это часто бывает со многими на первый взгляд простыми задачами, в ней скрыто немало тонкостей. Одной из таких замечательных тонкостей, мимо которой до сих пор проходили исследователи, является связь корней уравнений (3) и (4) с углами трех замечательных треугольников.

Чтобы убедиться в этом, рассмотрим, каким образом одномерный отрезок, разделенный в пропорции золотого сечения, может быть легко преобразован в двумерный образ в виде треугольника. Для этого, используя вначале рис. 1, отложим на отрезке АВ длину отрезка a дважды - от точки А в сторону точки В и, наоборот, от точки В в сторону А . Получим две точки С 1 и С 2 , делящие отрезок АВ с разных концов в пропорции золотого сечения (рис. 3). Считая равные отрезки АС 1 и ВС 2 радиусами, а точки А и В центрами окружностей, проведем две дуги до их пересечения в верхней точке С . Соединив точки А и С , а также В и С, получим равнобедренный треугольник АВС со сторонами АВ = a + b = 1, АС = = ВС = a = d ≈ 0,618. Величину углов при вершинах А и В обозначим α, при вершине С - β. Вычислим эти углы.

По теореме косинусов

(АВ ) 2 = 2(АС ) 2 (1 - cos β).

Подставив численные значения отрезков АВ и АС в эту формулу, получим

Аналогично получаем

(8)

Выход золотой пропорции на двумерный образ позволил связать корни уравнений (3) и (4) с углами треугольника АВС , который можно назвать первым треугольником золотой пропорции.

Выполним аналогичное построение, используя рис. 2. Если на продолжении отрезка АВ отложить от точки В вправо отрезок, равный по величине отрезку a , и повернуть вокруг центров А и В вверх оба отрезка как радиусы до их соприкосновения, то получим второй треугольник золотой пропорции (рис. 4). В этом равнобедренном треугольнике сторона АВ = a + b = 1, сторона АС = ВС = D ≈1,618, и поэтому по формуле теоремы косинусов получаем

(9)

Угол a при вершине С равен 36 о и связан с золотой пропорцией соотношением (8). Как и в предыдущем случае, углы этого треугольника связаны с корнями уравнений (3) и (4).

Второй треугольник золотой пропорции служит основным составляющим элементом правильного выпуклого пятиугольника и задает пропорции правильного звездчатого пятиугольника (пентаграммы), свойства которых подробно рассмотрены в книге .

Звездчатый пятиугольник - фигура симметричная, и в то же время в соотношениях ее отрезков проявляется асимметрическая золотая пропорция. Подобное сочетание противоположностей всегда притягивает глубоким единством, познание которого позволяет проникнуть в скрытые законы природы и понять их исключительную глубину и гармонию. Пифагорейцы, покоренные созвучием отрезков в звездчатом пятиугольнике, выбрали его символом своего научного сообщества.

Со времен астронома И. Кеплера (XVII век) иногда высказываются различные точки зрения относительно того, что обладает большей фундаментальностью - теорема Пифагора или золотая пропорция. Теорема Пифагора лежит в основании математики, это один из ее краеугольных камней. Золотое сечение лежит в основании гармонии и красоты мироздания. На первый взгляд оно несложно для понимания и не обладает значительной основательностью. Тем не менее некоторые его неожиданные и глубокие свойства постигаются только в последнее время , что говорит о необходимости с почтением относиться к его скрытой тонкости и возможной универсальности. Теорема Пифагора и золотая пропорция в своем развитии тесно переплетаются одна с другой и геометрическими и алгебраическими свойствами. Между ними нет ни пропасти, ни принципиальных различий. Они не конкурируют, у них разные предназначения.

Вполне возможно, что обе точки зрения равноправны, так как существует прямоугольный треугольник, содержащий в себе разнообразные особенности золотой пропорции. Другими словами, существует геометрическая фигура, достаточно полно объединяющая два математических восхитительных факта - теорему Пифагора и золотую пропорцию.

Чтобы построить такой треугольник, достаточно продолжить сторону ВС треугольника АВС (рис. 4) до пересечения в точке Е с перпендикуляром, восстановленным в точке А к стороне АВ (рис. 5).

Во внутреннем равнобедренном треугольнике АСЕ угол φ (угол АСЕ ) равен 144 о, а угол ψ (углы ЕАС и АЕС ) равен 18 о. Сторона АС = СЕ = СВ = D . Используя теорему Пифагора, легко получить, что длина катета

Используя этот результат, легко приходим к соотношению

Итак, найдена непосредственная связь корня y 2 уравнения (4) - последнего из корней уравнений (3) и (4) - с углом 144 о. В связи с этим треугольник АСЕ можно назвать третьим треугольником золотой пропорции.

Если в замечательном прямоугольном треугольнике АВЕ провести биссектрису угла САВ до пересечения со стороной ЕВ в точке F , то увидим, что вдоль стороны АВ располагаются четыре угла: 36 о, 72 о, 108 о и 144 о, с которыми корни уравнений золотой пропорции имеют непосредственную связь (соотношения (7) - (10)). Таким образом, в представленном прямоугольном треугольнике содержится вся плеяда равносторонних треугольников, обладающих особенностями золотого сечения. Кроме того, весьма примечательно то, что на гипотенузе любые два отрезка, ЕС = D и СF = 1,0 находятся в соотношении золотой пропорции с FВ = d . Угол ψ связан с корнями D и d уравнений (3) и (4) соотношениями

В основу представленных выше построений равнобедренных треугольников, углы которых связаны с корнями уравнений золотой пропорции, положены исходный отрезок АВ и его части a и b . Однако золотое сечение позволяет моделировать не только описанные выше треугольники, но и различные другие геометрические фигуры, несущие в себе элементы гармоничных отношений.

Приведем два примера подобных построений. В первом - рассмотрим отрезок АВ , представленный на рис. 1. Пусть точка С - центр окружности, отрезок b - радиус. Проведем радиусом b окружность и касательные к ней из точки А (рис. 6). Соединим точки касания E и F с точкой С . В результате получим асимметричный ромб АЕСF , в котором диагональ АС делит его на два равных прямоугольных треугольника АСЕ и АСF .

Обратим более пристальное внимание на один из них, например на треугольник АСЕ . В этом треугольнике угол АЕС - прямой, гипотенуза АС = a , катет СЕ = b и катет АЕ = √ab ≈ 0,486, что следует из соотношения (2). Следовательно, катет АЕ является средним геометрическим (пропорциональным) между отрезками a и b , то есть выражает геометрический центр симметрии между числами a ≈ 0,618 и b ≈ 0,382.

Найдем значения углов этого треугольника:

Как и в предыдущих случаях, углы δ и ε связаны через косинус с корнями уравнений (3) и (4).

Заметим, что асимметричный ромб, подобный ромбу AECF , получается при проведении касательных из точки В к окружности радиуса a и c центром в точке А .

Асимметричный ромб AECF получен иным путем в книге при анализе формообразования и явлений роста в живой природе. Прямоугольный треугольник АЕС назван в этой работе "живым" треугольником, так как способен порождать наглядные образы, соответствующие различным структурным элементам природы, и служить ключом при построении геометрических схем начала развития некоторых живых организмов.

Второй пример связан с первым и третьим треугольниками золотого сечения. Образуем из двух равных первых треугольников золотой пропорции ромб с внутренними углами 72 о и 108 о. Аналогично объединим два равных третьих треугольника золотой пропорции в ромб с внутренними углами 36 о и 144 о. Если стороны этих ромбов равны между собой, то ими можно заполнить бесконечную плоскость без пустот и перекрытий. Соответствующий алгоритм заполнения плоскости разработал в конце 70-х годов ХХ века физик-теоретик из Оксфордского университета Р. Пенроуз. Причем выяснилось, что в получающейся мозаике невозможно выделить элементар ную ячейку с целым числом ромбов каждого вида, трансляция которой позволяла бы получить всю мозаику. Но самым замечательным оказалось то, что в бесконечной мозаике Пенроуза отношение числа "узких" ромбов к числу "широких" точно равно значению золотой пропорции d = 0,61803...!

В этом примере удивительным образом соединились все корни золотого сечения, выраженные через углы, с одним из случаев нетривиального заполнения бесконечной плоскости двумя элементарными фигурами - ромбами.

В заключение отметим, что приведенные выше разнообразные примеры связи корней уравнений золотой пропорции с углами треугольников иллюстрируют тот факт, что золотая пропорция более емкая задача, чем это представлялось ранее. Если прежде сферой приложения золотой пропорции считались в конечном итоге соотношения отрезков и различные последовательности, связанные с численными значениями ее корней (числа Фибоначчи), то теперь обнаруживается, что золотая пропорция может генерировать разнообразные геометрические объекты, а корни уравнений имеют явное тригонометрическое выражение.

Авторы отдают себе отчет, что высказанная выше точка зрения относительно изящества математических соотношений, связанных с золотой пропорцией, отражает личные эстетические переживания. В современной философской литературе понятия эстетики и красоты трактуются довольно широко и используются скорее на интуитивном уровне. Эти понятия отнесены главным образом к искусству. Содержание научного творчества в эстетическом плане в литературе практически не рассматривается. В первом приближении к эстетическим параметрам научных исследований можно отнести их сравнительную простоту, присущую им симметрию и способность порождать наглядные образы. Всем этим эстетическим параметрам отвечает задача, получившая название "золотая пропорция". В целом же проблемы эстетики в науке далеки от своего решения, хотя и представляют большой интерес.

Интуитивно чувствуется, что золотая пропорция все еще скрывает свои тайны. Некоторые из них, вполне возможно, лежат на поверхности, ожидая необычного взгляда своих новых исследователей. Знание свойств золотой пропорции может служить творческим людям хорошим фундаментом, придавать им уверенность и в науке и в жизни .

ЛИТЕРАТУРА

1. Шевелев И. Ш., Марутаев И. А., Шмелев И. П. Золотое сечение: Три взгляда на природу гармонии. - М.: Стройиздат, 1990. - 343 с.

2. Стахов А. П. Коды золотой пропорции. - М.: Радио и связь, 1984. - 152 с.

3. Васютинский Н. А. Золотая пропорция. - М.: Молодая гвардия, 1990. - 238 с.

4. Коробко В. И. Золотая пропорция: Некоторые философские аспекты гармонии. - М. - Орел: 2000. - 204 с.

5. Урманцев Ю. А. Золотое сечение // Природа, 1968, № 11.

6. Попков В. В., Шипицын Е. В. Золотое сечение в цикле Карно // УФН, 2000, т. 170, № 11.

7. Константинов И. Фантазии с додекаэдром // Наука и жизнь, 2001, № 2.

8. Шевелев И. Ш. Геометрическая гармония // Наука и жизнь, 1965, № 8.

9. Гарднер М. От мозаик Пенроуза к надежным шифрам . - М. : Мир, 1993.